이 포스트는 Do it 딥러닝 교과서 (윤성진 저)를 참고하여 만들어졌음!
확률적 경사 하강법 (SGD)는 역전파 알고리즘이 탄생했던 1980년부터 사용되던 초창기 알고리즘이다. SGD는 weights update를 위해 하나의 sample만을 사용하므로 메모리 사용을 최소화 할 수 있고, 온라인 학습시 데이터가 추가될 때마다 모델을 update할 수 있다는 장점을 가진다. 하지만 학습 과정에서 발생하는 다양한 상황에 대처하기 어렵고 학습 속도가 느리다는 단점을 갖는다. SGD가 가진 문제점들에 대해 살펴보는 것을 시작으로 optimization에 대해 공부해본다.
Learning rate
Learning rate(학습률)은 optimization 과정에서 한 update step당 이동하는 step size를 의미한다. SGD는 고정된 learning rate를 사용한다는 단점을 가진다. (향후 방식들은 학습 상황을 알고리즘이 인식하고 이에 맞게 자동으로 학습률을 조정하는 방식으로 개선되었다.)

딥러닝 학습에서 learning rate 설정은 아주 중요하다. 학습 초기에는 큰 learning rate로 최적해에 다가가야 하고, 학습이 어느정도 진행되면 learning rate를 줄여 세밀한 조정이 필요하다. 항상 일정한 폭을 가지고 학습을 진행하면 충분한 에포크를 진행했음에도 불구하고 최적해에 다가가지 못하거나, 곡면보다 step size가 너무 커서 최적해에 도달하지 못하고 발산할 수 있다. 이런 경우 learning rate를 낮추지 않으면 최적해에 영원히 도달할 수 없으므로 좋은 성능을 기대하기 어렵다.
Adaptive learning rate 적응적 학습률
loss function의 경사가 가파를 때는 적은 폭으로 천천히 이동하고, 경사가 완만한 경우에는 큰 폭으로 빠르게 이동하는 것이 일반적으로 좋다. 이처럼 loss function의 곡면 변화를 고려하여 learning rate를 자동으로 조정하는 방식을 adaptive learning rate라고 한다.
Saddle point 안장점

Optimization은 단편적으로 생각하면 loss function에서 기울기가 0인 지점을 찾는 과정이다. SGD의 또 다른 단점은 최대, 최소, 안장점을 서로 구분할 수 없다는 것이다. 즉, 기울기가 0인 임계점에 도달하면 그것이 최대, 최소, 안장점 중 어떤 것인지 파악하지 못하므로 학습이 종료된다.
$n$차원 공간에서 임계점에 도착했을 때 각 차원별로 이것이 최대일 확률은 $\frac{1}{2}$이고, 최소일 확률 또한 $\frac{1}{2}$이다. (안장점이 존재하기 위한 최소차원은 3차원이다. 2차원에서 발생하는 임계값은 반드시 최소 또는 최댓값이다) 그 임계점이 최소점이려면 주어진 $n$차원에서 전부 최소여야 하므로, 최소점일 확률은 $\frac{1}{2^n}$이고, 같은 논리로 최대점일 확률 또한 $\frac{1}{2^n}$이다.
임계점 중 최대, 최소를 제외하면 전부 안장점이므로 $n$ 차원 공간에서 임계점을 만났을 때 그것이 안장점일 확률은 다음과 같다.
$$P(\text{안장점}) = 1-\frac{1}{2^n}-\frac{1}{2^n}=1-\frac{1}{2^{n-1}} $$
따라서 손실함수의 차원 $n$이 크면 클수록 임계점을 만났을 때 그것이 안장점일 확률이 매우 증가한다.
일반적으로 임계점을 만났을 때 loss 값이 매우 크다면 최대점, 중간정도 값을 갖는다면 안장점, 아주 작은 loss를 갖는다면 최소점일 가능성이 높다.
위 사진에서 알 수 있듯이 안장점은 옆으로 조금만 움직여도 내리막길이 나타난다. 따라서 step이 이동하던 속도에 관성을 주면 쉽게 탈출할 수 있다.
여기부터는 다양한 최적화 알고리즘들에 대해 알아본다.
SGD 모멘텀
$$\begin{align} &\vec{v_{t+1}}=\rho \vec{v}_t + \Delta f(\vec{x}_t) \\ &\vec{x}_{t+1}=\vec{x}_t-\alpha \vec{v}_{t+1} \end{align}$$
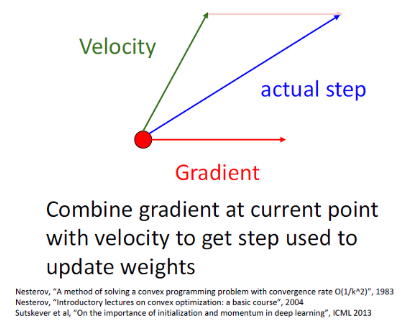
기존 SGD는 현재 위치에서의 gradient $\Delta f(\vec{x}_t)$만을 사용하여 update 한다. 하지만 SGD 모멘텀에서는 현재 속도 $\vec{v}_t$를 더하여 다음 속도벡터에 사용한다. 따라서 이 방식은 현재 이동하던 방향(속도벡터)을 $\rho$만큼 관성으로 반영한다는 의미다.
$\rho$는 마찰계수(friction coefficient)로 보통 0.9 혹은 0.99를 사용한다.

관성을 이용하여 update하는 경우 진행하던 속도로 계속 진행하려 한다. loss function의 표면이 울퉁불퉁한 경우 매 지점에서의 gradient는 사방팔방으로 튈 수 있는데 이때 관성의 영향으로 부드러운 이동이 가능하다. 또한 경사가 가파른 경우 gradient에 진행하던 속도를 더하여 더 빠른 속도로 경사를 내려갈 수 있다.
Overshooting
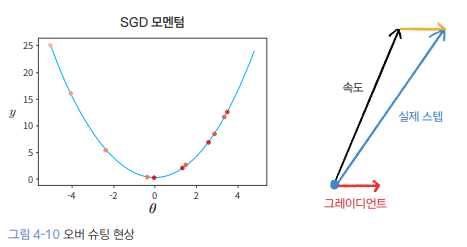
SGD momentum은 overshooting 문제가 발생할 수 있다. SGD momentum 식 $\vec{v}_{t+1}=\rho \vec{v}_t + \Delta f(\vec{x}_t)$에 의하면 급한 경사를 타고 내려갈 때 속도가 계속 누적된다. 이때 갑자기 경사가 완만해지는 지점을 만나면 gradient는 순간적으로 작아지지만 속도는 여전히 큰 값이므로 최소 지점을 지나쳐 발산하는 오버슈팅이 발생한다.
Nesterov momentum (네스테로프 모멘텀)
Nesterov momentum은 관성을 이용한다는 점에서 SGD momentum과 같지만 overshooting을 막기 위해 현재 속도로 한 걸음 미리 이동해보고 오버슈팅이 발생한 만큼 다시 되돌아오는 방식이다.
$$\begin{align} &\vec{v}_{t+1}=\rho \vec{v}_t-\alpha \Delta f(\vec{x}_t+\rho \vec{v}_t) \\ &\vec{x}_{t+1} = \vec{x}_t + \vec{v}_{t+1} \end{align}$$
위 식에서 $f(\cdot)$안의 $\vec{x}_t+\rho \vec{v}_t$는 현재 위치에서 SGD momentum을 이용해 한 걸음 앞으로 이동한 것을 의미한다. 따라서 $\vec{v}_{t+1}=\rho \vec{v}_t - \alpha \Delta f(\vec{x}_t + \rho \vec{v}_t)$는 다음 step에 이동할 속도는 현재 속도 - 한 걸음 미리 이동했을 때의 gradient 라는 것이다.
AdaGrad (adaptive gradient)

loss function의 경사가 가파를 때 큰 폭으로 이동하면 최소점을 지나칠 수 있으므로 작은 폭으로 이동하여 촘촘히 탐색하고, 경사가 완만할 때는 큰 폭으로 빠르게 이동하여 탐색하는 것이 좋다. 곡면의 변화량은 기울기의 변화량으로 step을 이동하며 계산했던 기울기를 모아서 크기를 측정하면 얻을 수 있다.
$$\text{Gradient vector} = (\Delta f (\vec{x}_1), \Delta f(\vec{x}_2), \Delta f (\vec{x}_3), \cdots, \Delta f(\vec{x}_t)) $$
각 step에서의 기울기의 제곱합을 곡면의 변화량으로 사용할 수 있다.
$$\text{곡면의 변화량} = \vec{r}_{t+1} = \Delta f(\vec{x}_1)^2 + \Delta f(\vec{x}_2)^2 + \cdots + \Delta f (\vec{x}_t)^2 $$
AdaGrad 식은 다음과 같이 나타낼 수 있다.
$$\begin{align} &\vec{r}_{t+1} = \vec{r}_t + \Delta f(\vec{x}_t)^2 \\ &\vec{x}_{t+1} = \vec{x}_t - \frac{\alpha}{\sqrt{\vec{r}_{t+1}} + \epsilon} \odot \Delta f(\vec{x}_t) \end{align} $$
여기서 위 식 $\vec{r}_{t+1} = \vec{r}_t + \Delta f(\vec{x}_t)^2$를 보면 update가 이루어질 때마다 gradient 제곱 합 $\vec{r}_{t+1}$이 누적되어 계속 커진다. 따라서 step이 진행될수록 adaptive learning rate $\frac{\alpha}{\sqrt{\vec{r}_{t+1}} + \epsilon}$이 작아진다.
따라서 기울기 크기가 큰 지점을 계속 방문하면 gradient 제곱합 누적이 굉장히 커져 learning rate가 매우 작아진다. 만약 경사가 매우 가파른 위치 (gradient가 매우 큰 위치)에서 학습을 시작한다면 초반부터 learning rate가 작아져서 최소값에 도달하기 전에 학습이 조기중단 될 가능성이 있다. 이를 해결하기 위해 RMSProp가 제안되었다.
RMSProp (Root Mean Square propagation)
RMSProp는 AdaGrad에서 조기에 학습이 중단되는 문제를 해결하기 위해 곡면 변화량을 개선된 방식으로 측정하는 optimization 방식이다. $\rightarrow$ 곡면 변화량 계산 시 여태껏 지나왔던 모든 경로에 대한 변화량을 계산하는 것이 아니라 최근 경로의 변화량을 측정하면 곡면 변화량이 누적되어 계속 증가하는 것을 막을 수 있다.

RMSProp 식은 다음과 같이 주어진다.
$$\begin{align} &\vec{r}_{t+1} = \beta \vec{r}_t + (1-\beta) \Delta f(\vec{x}_t)^2 \\ &\vec{x}_{t+1} = \vec{x}_t - \frac{\alpha}{\sqrt{\vec{r}_{t+1}} + \epsilon} \odot \Delta f(\vec{x}_t) \end{align} $$
이 식이 어떻게 최근 경로의 곡면 변화량을 더 크게 반영하는지 알기위해 $\vec{r}_{t+1}$에 대한 점화식을 풀어본다.
$$\begin{align} \vec{r}_{t+1} &=\beta \vec{r}_t + (1-\beta) \Delta f(\vec{x}_t)^2 \\ &=\beta (\beta \vec{r}_{t-1} + (1-\beta)\Delta f(\vec{x}_{t-1})^2) + (1-\beta) \Delta f(\vec{x}_t)^2 \\ &= \beta^2 \vec{r}_{t-1} + \beta(1-\beta) \Delta f(\vec{x}_{t-1})^2 + (1-\beta) \Delta f(\vec{x}_t)^2 \\ &=\beta^2 \vec{r}_{t-1} + (1-\beta)(\Delta f(\vec{x}_t)^2 + \beta \Delta f(\vec{x}_{t-1})^2) \end{align} $$
위 식의 결과는 $\vec{r}_{t+1}$에 $\vec{r}_t$를 대입하여 얻은 것이다. $\vec{r}_{t-1}$부터 $\vec{r}_1$까지 전부 대입하면 다음과 같이 식이 정리된다.
$$\vec{r}_{t+1} = \beta^t \vec{r}_1 + (1-\beta)(\Delta f(\vec{x}_t)^2 + \beta \Delta f(\vec{x}_{t-1})^2 + \cdots + \beta^{t-1} \Delta f(\vec{x}_1)^2) $$
가장 최근 기울기 변화량인 $\Delta f(\vec{x}_t)^2$는 계수가 1으로 전부 반영되는 반면 가장 오래된 기울기 변화량 $\Delta f(\vec{x}_1)^2$는 계수가 $\beta^{t-1}$으로 가장 적게 반영되는 것을 알 수 있다. (일반적으로 $\beta=0.9$로 설정한다는 것을 고려하자)
Adam (Adaptive momentum estimation)
Adam은 관성(SGD momentum)과 적응적 학습률(RMSProp)의 장점을 전부 취하는 방식으로 개발되었다. Adam은 RMSProp의 학습 초기 경로가 편향되는 문제를 제거하여 최적화 성능이 더 우수하고 이상치에 대해 민감하게 반응하지 않는다는 장점을 갖는다.
$$\begin{align} &v_{t+1} = \beta_1 \vec{v}_t + (1-\beta_1) \Delta f(\vec{x}_t) \\ &\vec{r}_{t+1} = \beta_2 \vec{r}_t + (1-\beta_2) \Delta f(\vec{x}_t)^2 \\ &\vec{x}_{t+1} = \vec{x}_t - \frac{\alpha}{\sqrt{\vec{r}_{t+1}}+\epsilon} \odot \vec{v}_{t+1} \end{align}$$
여기서 $\beta_1, \beta_2$는 일반적으로 0.9 혹은 0.99를 사용한다.
첫 번째 식을 살펴보면 현재 위치에서의 속도를 $\beta_1 \vec{v}_t$만큼, 현재 위치에서의 gradient를 $(1-\beta_1) \Delta f (\vec{x}_t)$만큼 반영한다. $\beta_1$를 0.9 정도로 사용하므로, 현재 위치의 gradient보다는 관성에 더 많은 가중을 주어 이동한다는 것을 알 수 있다. (SGD momentum : $\vec{v}_{t+1} = \rho \vec{v}_t + \Delta f(\vec{x}_t)$)
두 번째 식 $\vec{r}_{t+1}=\beta \vec{r}_t + (1-\beta) \Delta f (\vec{x})^2$는 RMSProp에서의 gradient 누적과 동일하다. 따라서 과거 step에서 얻어진 기울기 변화율보다 최근 step에서 얻어진 기울기 변화율을 더 큰 비중으로 반영한다. 또한 이 식 역시 다음 step에서 사용되는 값 $\vec{r}_{t+1}$을 구하는 데 현재 값 $\vec{r}_t$를 반영하므로 관성 개념을 사용한 것이다.
마지막 update 식은 RMSProp 식 ($\vec{x}_{t+1}=\vec{x}_t - \frac{\alpha}{\sqrt{\vec{r}_{t+1}} + \epsilon} \odot \Delta f (\vec{x}_t)$)와 거의 유사하다. 다만 차이점이 있다면 Adam에서는 관성을 갖는 속도 $\vec{v}_{t+1}$을 사용한다.
위 식을 그대로 사용하면 첫 step에서 출발 지점에서 멀리 떨어진 곳으로 이동하는 '초기 경로의 편향' 문제가 발생한다. 해당 문제가 발생하는 이유를 수식으로 살펴보자.
$$\begin{align} &\beta_1 = 0.9, \; \beta_2 = 0.99 \\ &\vec{v}_0 = 0, \; \vec{r}_0=0 \\ &\text{for t in range(1, num_iterations):} \\ &\quad \vec{v}_{t+1} = \beta_1\vec{v}_t + (1-\beta_1) \Delta f (\vec{x}_t) \\ &\quad \vec{r}_{t+1} = \beta_2 \vec{r}_t + (1-\beta_2) \Delta f(\vec{x}_t)^2 \\ &\quad \vec{x}_{t+1} = \vec{x}-\frac{\alpha}{\sqrt{\vec{r}_{t+1}} +\epsilon} \odot \vec{v}_{t+1} \end{align}$$
$\beta_1 =0.9, \beta_2 = 0.99$로 설정하여 위 Adam을 사용한 경우 $\vec{r}_1 = 0.01 \Delta f(\vec{x}_0)^2$이 된다. 따라서 $\vec{x}_{t+1}$이 $\vec{x}_t$와 매우 멀리 떨어진 값이 될 수 있다. 이때 운이 좋지 않으면 최소값과 동 떨어진 곳에 놓여지므로 영 좋지못한 일이다.
사실 이 초기 경로의 편향 문제는 RMSProp에서 발생하는 문제이다. Adam에서는 이를 제거하기 위하여 $\vec{v}_{t+1}=\frac{\vec{v}_{t+1}}{(1-\beta_1^t)}, \vec{r}_{t+1} = \frac{\vec{r}_{t+1}}{(1-\beta_2^t)}$를 사용한다. 이 식을 사용했을 때 어떻게 초기 경로의 편향 문제가 사라지는지 수식으로 살펴본다.
$$\begin{align} &\beta_1 =0.9, \beta_2 =0.99 \\ &\vec{v}_0 = 0, \vec{r}_0 = 0 \\ &\text{for t in range(1, num_iterations):} \\ &\quad \vec{v}_{t+1} = \beta_1\vec{v}_t + (1-\beta_1)\Delta f(\vec{x}_t) \\ &\quad \vec{r}_{t+1}=\beta_2 \vec{r}_t + (1-\beta_2)\Delta f(\vec{x}_t)^2 \\ &\quad \vec{v}_{t+1} = \frac{\vec{v}_{t+1}}{(1-\beta_1^t)} \\ &\quad \vec{r}_{t+1} = \frac{\vec{r}_{t+1}}{(1-\beta_2^t)} \\ &\quad \vec{x}_{t+1} = \vec{x}_t - \frac{\alpha}{\sqrt{\vec{r}_{t+1}} + \epsilon} \odot \vec{v}_{t+1} \end{align}$$
원리는 매우 간단하다. 그냥 위에서 $\vec{v}_1=0.1 \Delta f(\vec{x}_0)$, $\vec{r}_1=0.01 \Delta f(\vec{x}_0)^2$으로 도출되어 $\vec{r}_1$ 값이 작아지는 문제를 제거하기 위해 앞의 계수 0.01을 제거했다고 보면 된다. 따라서 개선된 방식을 사용하면 $\vec{v}_1 = \Delta f(\vec{x}_0)$, $\vec{r}_1 = \Delta f(\vec{x}_0)^2$을 얻는다. $\vec{r}_1$이 gradient의 제곱이 되므로 아주 작아질 일이 없기 때문에 학습 초반에 learning rate가 급격히 커지는 편향이 제거된다.
또한 $\beta^t_1, \beta^t_2$에서 $t$가 커질수록 ($t$는 step 횟수를 의미한다. 즉 학습이 진행된 정도를 의미) 0으로 수렴하므로 분모의 $(1-\beta^t_1)$와 $(1-\beta^t_2)$는 학습 초기에만 작용하고, 학습이 진행될수록 원래 알고리즘으로 돌아간다.
'딥러닝' 카테고리의 다른 글
| 11. 컨볼루션 신경망, CNN (Convolution neural network) (0) | 2023.09.27 |
|---|---|
| 9. 초기화 Initialization (0) | 2023.09.21 |
| 7. 손실함수 Loss function (0) | 2023.09.15 |
| 6. 배치, 미니배치, SGD (0) | 2023.09.15 |
| 5. 경사하강법, 역전파 알고리즘 (0) | 2023.09.15 |


