이 게시글은 K-mooc 고영채교수님의 이동통신공학 1을 수강한 내용을 바탕으로 작성하였음
-
System capacity in cellular system
-
Improving the system capacity
-
Introduction to channel models
-
Categorization of channel models
System capacity in cellular system
Cellular system에서의 system capacity라는 것에 대한 정의를 내리고 이것이 어떻게 전개되는지 살펴볼 것이다.
Co-channel Interference
Cellular system의 가장 핵심 개념은 frequency reuse라는 것을 알아보았다. Cellular의 기본적인 개념은 1970년대 bell lab의 한 연구원에 의해 고안된 아이디어이다. 1970년대는 오늘날처럼 누구나 스마트폰을 사용하는 광경을 공상과학 영화에서나 보며 상상하던 시기이다. 그 시기에 한정된 BW를 어떻게 효율적으로 사용해야 할 지에 대한 Cellular system 아이디어가 처음 고안되었는데, 이것은 20~30년이 흐른 1990년대에 구현되었다.
따라서 지금 우리가 상상하고 있는 많은 것들도 20~30년 후에는 실제로 이루어질 수 있다.

위 그림은 Cluster 개수 $N=1$일 때의 Cellular system이다. $N=1$인 경우에는 모든 cell들이 같은 BW를 사용하기 때문에 인접한 cell간 간섭이 발생하게 되고, 이것을 co-channel interference라고 부른다.
- 같은 BW를 사용하는 인접 cell간 중심거리 $D$ : Reuse distance
- 한 cell의 반지름 $R$ : cell distance
- : cluster size

Co-channel factor $Q$는 다음과 같이 쓸 수 있다.
$$Q=\frac{D}{R}=\sqrt{3N}$$
통신사업자가 cell을 디자인 할 때, 한 cell의 반지름 $R$은 고정시켜두고, $D$를 바꿔가며 $Q$를 측정한다. reuse cell간 거리 $D$를 1km로 할지 10km로 할지 바꿔가며 system의 특성을 결정하는 것이다.
($R$ cell의 크기가 변해서 필연적으로 $D$도 변하므로, $R$과 $D$를 동시에 변화시키며 비교하는 건 매우 복잡하다. 하나를 고정시켜야 함)
을 고정한 상태에서 $D$를 늘리면 $Q$값이 커진다. $Q$값이 커지면 Co-channel interference가 낮다.
→ 같은 BW를 사용하는 cell간 물리적 거리가 멀어지기 때문에 co-channel interference가 줄어드는 것이다.
→ $D$ Co-channel interference ↓
오른쪽 그래프는 $Q$값을 일정하게 고정시켰을 때 $R$과 $D$의 관계를 $N$의 변화에 따라 나타낸 것이다. $Q=\frac{D}{R}=\sqrt{3N}$이므로 각 그래프의 기울기는 $\sqrt{3N}$이다.
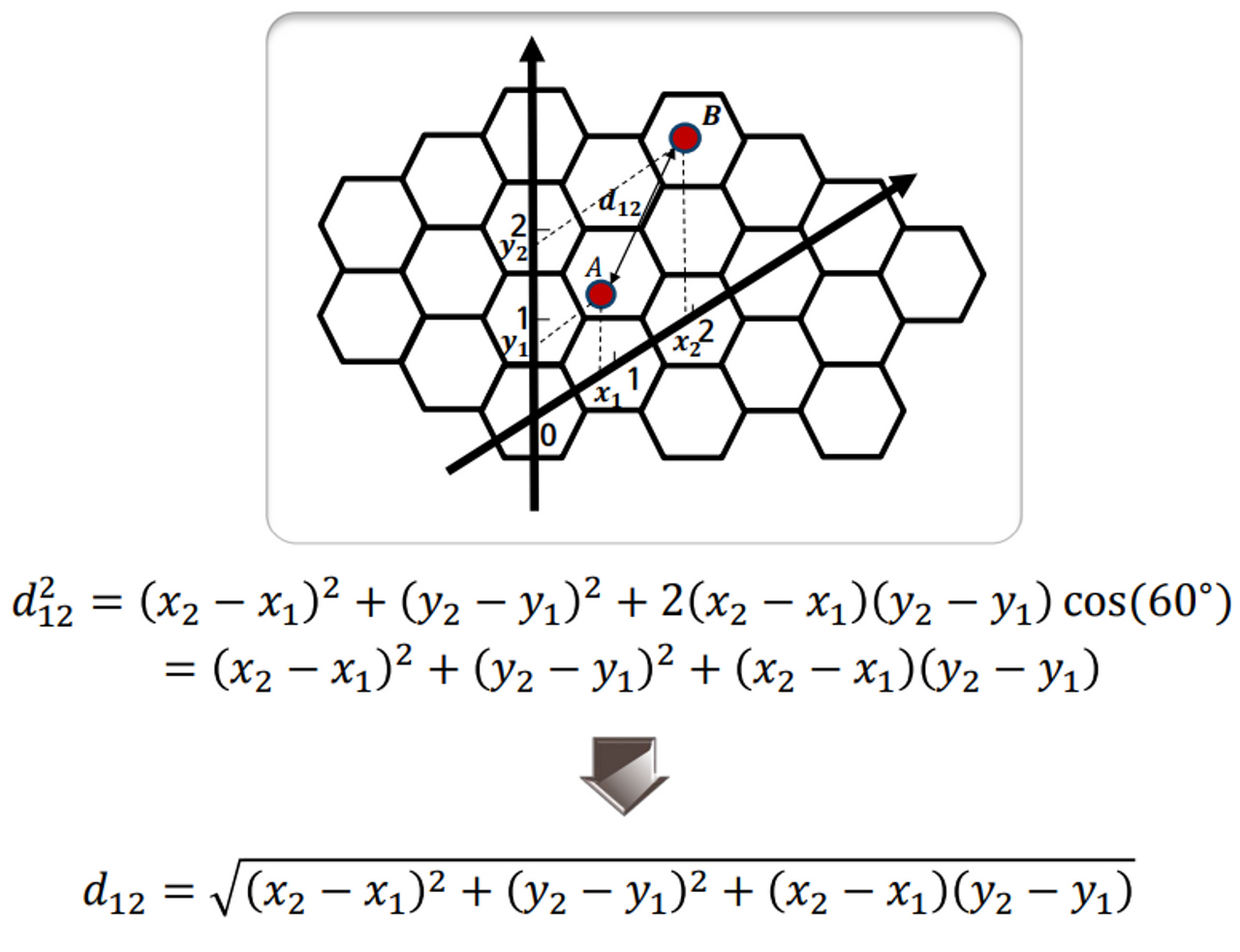
Co-channel factor $Q=\frac{D}{R}=\sqrt{3N}$ 식을 한 번 유도해본다.
- x축과 y축을 좌표상에 나열된 cell들의 중심점을 지나도록 재설정한다. 기존의 Orthogonal한 좌표축은 x축과 y축이 이루는 각도가 90도이지만, 이 경우에는 두 축이 이루는 각도가 60도이다.
- 좌표축에서 (1,1) 위치에 있는 cell A의 좌표를 ($x_1, y_1$)으로 두고, (2,2) 위치에 있는 cell B의 좌표를 ($x_2, y_2$)로 둔다. 여기서 (1,1)이라고 함은 cellular 좌표계 상에서 첫번째 x, 첫번째 y 값을 가진다는 것을 의미하며 scalar 1을 의미하는 것이 아니다. 좌표계가 달라졌음에 주의
- A와 B 사이의 distance $d_{12}$는 피타고라스 정리를 이용하면 다음과 같이 얻어진다.
$(x_1, y_1)=(\sqrt{3}R, \sqrt{3}R), (x_2, y_2)=(2\sqrt{3}R, 2\sqrt{3}R)$으로 두면 $d_{12}$는 다음과 같이 다시 쓸 수 있다. 이때 $R$은 한 cell의 radius를 의미한다.
$d_{12}=\sqrt{3}R\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(x_2-x_1)(y_2-y_1)}$
쉽게 말해서 cellular 좌표계에서 두 점간 거리는 $\sqrt{3}R$에 두 좌표의 거리를 곱한것과 같다. 이제 한 cell A (i,j)가 존재할 때 A와 인접한 cell B가 존재한다고 해보자. B는 A와 바로 옆에 존재하므로 좌표가 (i+1, j+1)이 된다. 왜? A랑 B가 바로 옆에 있다는 게 이해가 안 됨 이때 A(1,1)와 B(2,2) 간 거리를 위 식에 대입하여 계산해보면 $d=3R$를 얻을 수 있다. 따라서 인접한 두 cell간 거리 : $d=3R$

같은 BW를 사용하는 인접한 cell간 거리를 $D$ : reuse distance로 설정하였었다.
(0,0) 원점에 빨간색 BW를 사용하는 cell이 존재하고, 동일한 BW를 사용하는 다음 cell이 (i,j)에 위치해있을 때 두 cell간 distance $D$는 다음과 같다.
지난 시간에 cluster size $N$은 아무 값이나 될 수 있는 게 아니라, $N=i^2+j^2+ij$ 를 만족하는 특수한 경우에만 $N$이 될 수 있다는 것을 배웠다. 따라서 다음과 같이 식을 다시 쓸 수 있다.
여기서 $\frac{D}{R}$을 Co-channel factor $Q$로 정의한다.
Co-channel interference

Co-channel interference가 BER 성능에 미치는 영향은 매우 상당하다. 두 cell이 동일한 BW를 사용하면 성능을 저하시키는 요인이 되는데, Cellular system에서는 그것에 대한 척도를 co-channel factor로 설정하는 것이다.
$Q=\frac{D}{R}=\sqrt{3N}$값이 높다 : co-channel interference가 매우 낮아서 성능이 좋다. : Quality of service가 좋다
값이 낮다 : cluster size N값이 작다 : co-channel interference가 높다 : 성능이 나쁘다
Channel Bandwidth in LTE

위 표는 어떤 Internet service provider의 LTE 표준(cellular system)이다. 이 사업자는 Downlink로 2110~2170MHz를, Uplink로 1920~1980MHz를 사용한다. : 각각 60MHz이다.
이때 한 사람당 사용할 수 있는 channel BW는 5, 10, 15, 20MHz 중 하나로 선택된다.
한 사람당 5MHz를 사용할 수 있다면 60MHz를 동시에 총 12명이 나눠쓸 수 있다. (DL, UL 둘 다 60MHz이므로 둘 다 12명이 나눠쓸 수 있음)
이 상황을 그림으로 보면 다음과 같다.

일단 BW를 총 12개의 channel으로 나눈다. N=4인 Cellular system을 사용한다면 총 12개의 channel을 다시 각 cluster들에 분배해야 하는데, 한 cluster 당 4개의 cell을 가지므로 한 cell이 사용할 수 있는 channel은 3개이다. (같은 색에 해당하는 cell은 같은 channel 3개를 공유한다)
우리는 무전기를 사용하는 것이 아니므로 Uplink, Downlink를 pair로 묶어서 동시에 사용해야 하기 때문에 1 duplex channel = 1 Uplink + 1 Downlink로 생각한다.
Cluster size and Duplex channels

하나의 duplex channel이 사용하는 BW=5MHz로 설정했기 때문에 총 60MHz의 BW가 존재할 때 이를 12개의 duplex channel이 나눠서 사용할 수 있다.
Cellular system의 한 cluster 당 cell의 개수가 4개라면 12개의 duplex channel을 4개의 cell이 나눠 사용해야 하므로, 한 cell당 3개의 duplex channel을 사용한다. → $k=3$

따라서 한 cluster당 총 Duplex channel 개수 $S$는 cluster size $N$에 한 cell당 사용하는 duplex channel 수 $k4를 곱한 것과 같다. Cluster size $N$ : 한 cluster에 존재하는 cell 개수

Cellular system은 어떤 지역 전체를 커버하기 위해 한 cluster 묶음의 복사본을 $M$개 가진다. 그 지역에서 동시에 통신 system을 사용할 수 있는 사람의 숫자는 $C=M\times S$가 되며 이것을 System capacity라고 한다.
<$M$: 어느 지역의 cluster 총 개수, $S$: 한 cluster당 사용 가능한 duplex channel 수>
통신 사업자는 가능한 많은 사용자들에게 서비스를 제공하여 이득을 취해야 하므로 통신 사업자에게 system capacity는 매우 중요한 지표이며 사업의 성공 여부를 결정짓는다.
Improving the system capacity
System capacity는 한정된 BW를 얼마나 많은 사용자들에게 분배할 수 있는지에 대한 척도였다. 그렇다면 cellular system에서 어떻게 해야 이 capacity를 증가시킬 수 있는지에 대한 탐구가 이루어져야 한다.
우리는 $S$(한 cluster당 배정된 duplex channel 수)를 늘릴 수 없다. 즉, 사업자가 가지고 있는 BW가 한정되어 있고, 한 사람이 사용할 수 있는 BW 또한 5MHz 혹은 10MHz 정도로 정해져 있기 때문에 cluster당 duplex channel 값 $S$를 임의로 조정할 수는 없다.
(한 cluster는 사업자가 제공하는 BW를 모두 사용한다.)
Capacity $C=M\times S$로 정해지므로, $C$를 증가시키기 위해서는 $M$을 늘려야 한다. ($M$ = cluster 반복 횟수)
Increasing M by Small Cluster size

Cell의 반경 $R$이 동일하고, 지역의 총 넓이가 동일할 때 한 cluster에 존재하는 unique한 cell의 수 $N$이 작을수록 cluster의 크기 자체가 작아지기 때문에 전체 지역을 cover하기 위해서는 cluster를 더 많이 반복해야하며 그에따라 $M$이 증가한다.
즉, $N$값을 작게 설정할수록 frequency reuse 횟수가 증가하여 Capacity도 증가한다. 하지만 $N$값이 작아질수록 같은 BW를 사용하는 cell간 거리가 가까워져 Co-channel interference가 증가한다.
인 cluster를 사용하고 있다. $N$을 최대한으로 낮춰 system capacity를 최대한으로 사용하고 있는 것이다.
Increasing M by Small Cell Radius

$N$이 고정되어있을 때 cell의 반경 $R$값을 줄이면 cluster가 해당 지역을 cover하기 위해서는 더 많은 반복이 필요하므로 $M$이 증가한다.
위 그림에서 $R$을 절반으로 감소시키는 경우 $M$이 4배 증가한 것을 확인할 수 있다. → 이 경우에도 $R$값이 작아짐에 따라 co-channel interference 증가 하냐? ㄴㄴ $N$이 일정해서 똑같다.
여기서 $R$이 줄어들면 $Q=\frac{D}{R}$가 커져서 interference가 작아지는 것이 아니냐는 의문을 가질 수 있는데, $R$이 감소하면 $D$도 반드시 감소하기 때문에 $Q$가 일정하다
이처럼 cell size를 작게해서 작은 cell들이 많은 횟수로 반복되게 하는 구조를 small cell 기법이라고 하며, 이는 5G의 핵심기술 중 하나이다.
만약 하나의 cell이 BS를 포함한 넓은 지역을 cover하는 것이 아니라, 한 가정당 하나의 cell을 가질 정도로 cell 크기를 매우 작게 줄인다면 system capacity를 매우 증가시킬 수 있으므로 5G에서는 small cell이 사용될 것으로 전망된다.
Trade-off Between Quality and Capacity
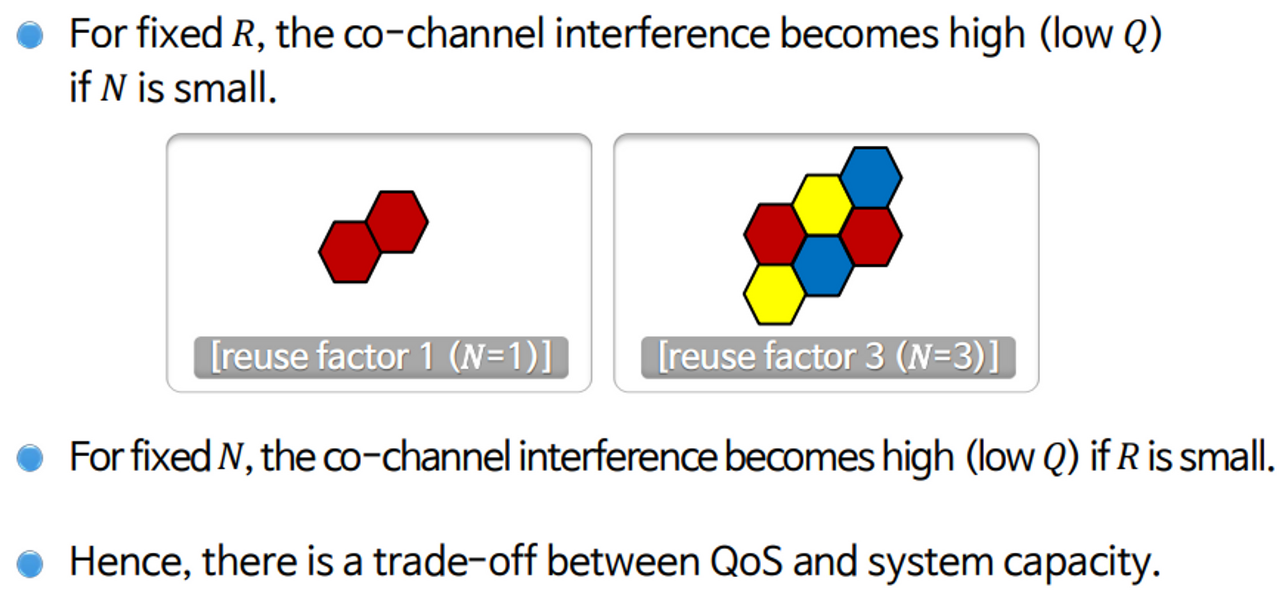
높은 Capacity를 위해 $M$값을 증가시키려고 $N$을 낮추는 경우 $Q$값이 작아져서 co-channel interference가 발생할 가능성이 매우 높아진다고 했다.
Small cell을 사용하는 경우에도 인접 cell간 거리가 가까워지므로 co-channel interference가 큰 영향을 미칠 수 있다. 따라서 Quality와 System Capacity간 trade-off가 존재한다.
Quality of service를 향상시키기 위해 동일 BW를 사용하는 cell 간 거리를 떨어뜨리면 Capacity가 감소하여 한 번에 많은 사용자를 수용할 수 없다.
Improving Capacity by Sectoring the cell

Omni directional antenna는 x-y평면을 기준으로 360도로 power를 전파하는 안테나이다. 이 안테나의 전파 영역을 120도, 90도, 60도로 분할(Sectoring)하여 frequency reuse를 증가시킬 수 있다.
120도 sector를 사용하는 경우에는 세 개의 영역 a,b,c에 대하여 각각 120도씩 담당하는 안테나를 총 3개 설치한다. 이때 각 영역은 서로 다른 BW를 사용한다.

120도 Sectoring을 사용하는 경우 sectoring을 하지 않았을 때보다 frequency reuse가 3배 증가하므로 Capacity 역시 3배 증가한다. 이 기술은 3G에서 시작되어 현재 LTE에서도 사용되고 있다.
Trend of Cell Size

예전 2G 시절에는 Macro-cell을 사용하여 한 cell당 1~10km의 반경을 가졌었다. 그 이후 사용자가 점점 많아지면서 cell size를 줄여나가고 있고, 5G에서는 Pico, Femto-cell 보다 더 작은 cell이 구현될 수도 있다는 전망이다.
Introduction to channel models
Mobile Radio Propagation

Wireless comm에서 Tx와 Rx를 어떻게 설계할 것인가에 대한 많은 이유를 바로 channel model에서 찾을 수 있다. 즉, channel model은 이동통신 system을 이해하는 데 가장 중요한 부분이라고 말할 수 있다.
Wired comm과는 다르게 Wireless comm에서는 scattering(산란), diffraction(굴절), reflection(반사)가 일어나기 때문에 Rx에서 원본 신호를 예측하기가 매우 어려워진다. 더불어 Tx가 고정돼있을 때 (BS는 움직이지 않으므로) Rx가 계속 움직인다면 (Mobility가 있다면) 주변 환경이 시간에 따라 계속 변화하여 received signal의 power가 계속 달라진다.
Channel model은 Tx에서 보낸 신호와 Rx에서 받은 신호의 관계를 특정짓는 역할을 하기 때문에 channel model을 파악하는 것이 wireless comm에 있어 아주 중요한 요소가 된다.
Goal

Tx와 Rx사이에는 무수히 많은 물리적 장애물들이 있고, 그것들에 의해 scattering, diffraction, reflection이 발생하고, 심지어는 이것들이 시간에 따라 변한다. 이 모든 복잡한 요소들을 하나의 수학적 모델 wireless channel으로 표현한다.
Digital comm review

Voice comm을 예시로 들어보면 comm system의 process는 다음과 같다.
- 마이크에 음성신호가 들어오면, 음성신호가 전기신호로 변환된다. → 원본 아날로그 신호가 전류 혹은 전압의 analog electrical signal로 변환된다.
- 얻어진 Analog electrical signal을 Digital 신호로 바꾸기 위하여 먼저 sampling 과정을 거친다. Sampling을 거친 신호는 여전히 analog이다. 가질 수 있는 Y값이 무한하므로, discrete time analog 신호이다.
- Quantization을 거치면 Y값 역시 discrete가 되므로 이때부터 digital signal이라고 부를 수 있다. Quantization level을 높일수록 원본 analog signal과 근접한 값을 얻을 수 있다.
- Quantization 된 signal를 amplitude를 구간별로 나눠 bits 단위로 encoding 한다. Rx에서 원본신호의 bits를 완벽하게 복원할 수 있다면 Received signal은 원본 신호와 동일한 정보를 갖고 있다고 말할 수 있다. (Quantization noise 제외)

실제로 channel에 신호를 전송할 때는 binary bits를 전송할 수가 없다. 0 1 0 1의 숫자 나열은 어떠한 형체도 가지고 있지 않기 때문이다. 그렇기에 bits들을 적절한 RF analog symbol로 Modulation한 후 전송한다.
Analog 원본 신호를 보내는 것에 비해 위 과정은 다소 복잡하지만, 성능을 매우 높은 수준으로 개선할 수 있다.
Symbol duration이 동일할 때 한 symbol에 더 많은 bits를 실어 보내면 Data rate를 증가시킬 수 있다. 하지만 BER 성능 역시 나빠져 error가 더 많이 발생한다.
$s_1(t)=-a \dot p(t )\cos (2\pi f_c t)$에서 $p(t)$는 analog 신호를 구성하기 위한 pulse를 나타내고, $\cos (2\pi f_ct)$는 RF 대역으로 신호를 올려보내기 위한 역할을 수행한다.

Wireless comm에서는 scattering diffraction, reflection에 의해 그냥 대놓고 noise가 판을 친다. Wired comm은 wireless와 비교하여 매우 원활한 통신이 가능하지만 noise가 없는 것은 아니다. 전자기기에 열이 발생함에 따라 Thermal noise가 항상 발생하므로, noise에 대한 수학적 modeling이 반드시 필요하다.
Rx에는 원본신호에 noise가 추가된 수신신호 $r(t)$를 받게 되는데, 이를 Matched filter를 거친 후 Optimum detector를 이용하여 error를 최소화하여 optimal한 결정을 내린다.
Received signal in wireless channels
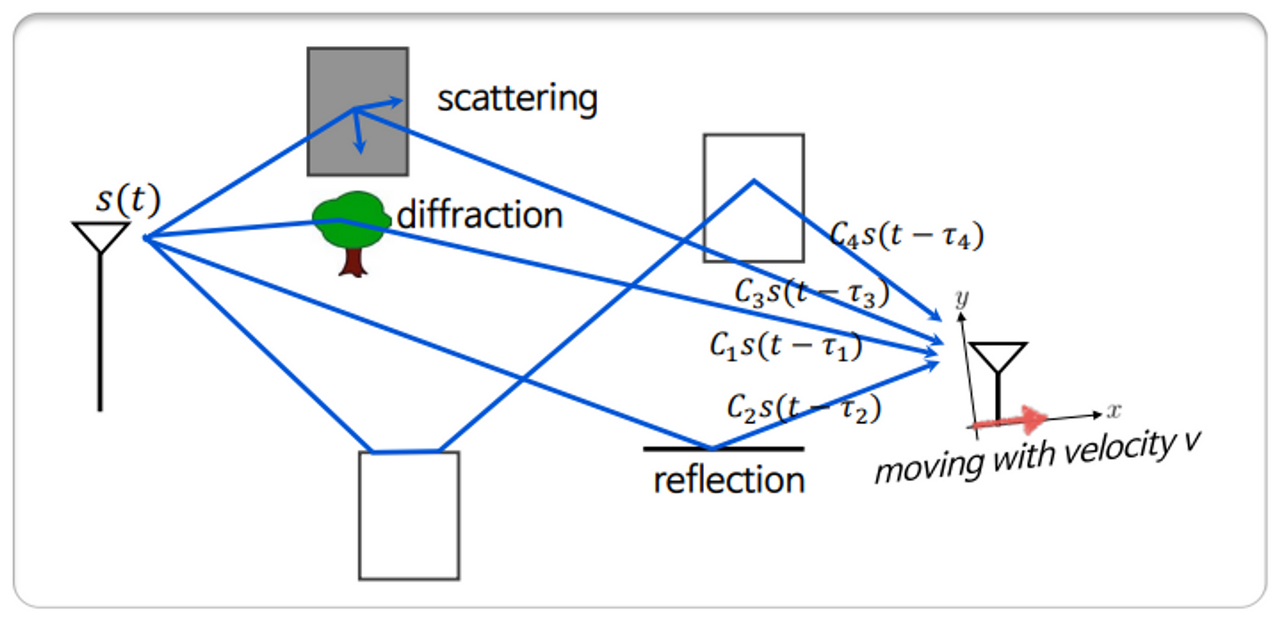
Wireless channel을 어떻게 modeling할 수 있는지 알아본다.
Tx에서 보낸 신호 $s(t)$는 channel에 존재하는 장애물들에 의해 delay되어 Rx에 도착한다. 이때 신호들은 순서대로 $C_1s(t-\tau_1), C_2s(t-tau_2) \cdots$의 channel과 곱해진 후 Rx에 도착하여 더해진다고 이해할 수 있다.
: Attenuation factor
: Delay factor
예를 들어 산에 올라가서 야호라고 소리쳤을 때
$C_1s(t-tau_1)$ → 내가 소리치는 순간 들은 신호 : 감쇠가 없으므로 $C=1$
$C_2s(t-tau_2)$ → 가장 가까운 산으로부터 반사된 메아리
$C_3s(t-tau_3)$ → 그 다음 도착한 메아리
더하여 Rx는 mobile 기기이므로, Rx가 움직일 때는 반사된 신호들이 모두 변형되어 도착하므로 원본 신호 $s(t)$를 복원하기가 더 어려워진다.
Instantaneous and Average Powers of Received signal
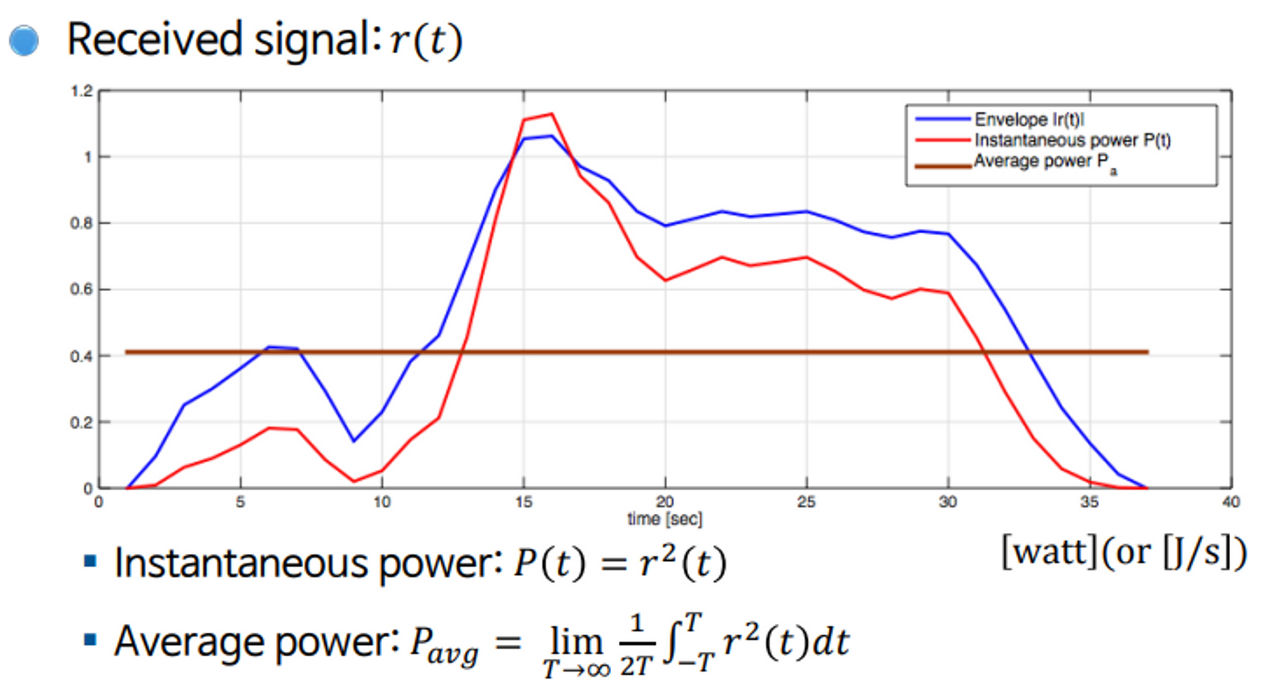
통신이 잘 된다는 것은 Received signal의 크기가 크다는 말과 동치이다. 크게 말하면 더 잘들리는 것과 같은 원리이다. Rx 안테나에 들어오는 신호의 세기가 적당히 크다면 noise의 영향을 어느정도 무시할 수 있으므로 통신하는 데 문제가 없다.
어떤 signal의 Instantaneous power는 그냥 신호를 제곱해버리면 된다.
$P(t)=r^2(t)$
Instantaneous power를 time에 따라 average를 취하면 Average power를 얻는다.
$P_{avg}=\lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^{T}r^2(t)dt$
$r(t)$는 정현파이므로 한 주기에 대한 average를 구한다.
위 그림에서 파란색 선은 $|r(t)|$로, received signal $r(t)$의 envelope를 나타낸다. 빨간색 선은 $r(t)$ Instantaneous power로, 매 시간 환경들이 변화됨에 따라 값이 출렁이는 것을 볼 수 있다.
갈색 선은 average power를 나타낸다.
Mathematical Model of Wireless Channel

Wireless channel에서 발생하는 scattering, diffraction, reflection등의 모든 요소를 black box $f[ \dot]$에 넣어놓고, black box의 input이 $s(t)$일 때 output을 $f[s(t)]$로 정의한다.
우리가 $f[ \dot]$을 정확히 알 수 있다면, $f$에 대한 역함수를 취하여 $r(t)$로 부터 $s(t)$를 그대로 복원해낼 수 있다. ($n(t)$가 충분히 작은 경우)
$$f를 잘 알아내기 위해서 즉, 채널 예측을 잘 하기 위해서는 일단 channel model이 필요하므로, 앞으로 이에 대해 공부해본다.
Categorization of channel models
Wireless channel은 매우 복잡한 형태로 구성된다. 이 복잡한 형태를 수학적으로 정확히 modeling할 수 있다면 수신된 신호를 보고 원본 신호를 온전하게 detection 할 수 있다. channel modeling을 효율적으로 진행하기 위해 modeling process를 어느정도 구분한 후에, 단계적으로 modeling하고자 한다.
(AWGN을 논외로 했을 때) $s(t)$는 channel에 의해 $r(t)$로 변화하여 Rx에 도착한다. 따라서 channel이 어떤 형식으로 나타나는지 정확하게 예측할 수 있다면, Rx의 mobility가 어떻든 간에 $f$라는 channel 함수를 정확하게 알 수 있다면 역함수를 이용하여 $r(t)$에서 $s(t)$를 얻을 수 있다.
Received Average Power in Free Space

먼저 Tx와 Rx간 distance에 따라 신호의 power가 약해진다는 사실을 알고있다. Free space에서 $X$라는 power를 전송한다면 Tx에서 $d$만큼 떨어진 Rx에서 $G(X)$를 수신한다. 즉 $G(\dot)$는 distance에 따라 power가 얼마나 감쇠되는지를 나타내는 함수이다.
Received Average Power with Obstacles

이번에는 Free space가 아니라 장애물이 존재하는 경우이다. Tx와 Rx간 거리는 $d$로 위 예시와 동일하다. 이때는 Tx에서 $X$라는 power를 전송하는 경우 Rx에서는 $G'(X)$을 수신한다. 그렇다면 $G(X)$는 $G'(X)$와 같을 것인가?
→ 아니다. 같은 거리 $d$ 만큼 떨어져 있다 하더라도 경로상에 장애물이 존재하지 않는 경우와 장애물이 존재하는 경우를 비교했을 때 수신하는 power의 크기는 다를 것이다.

세 번째 경우이다. $r_1$과 $r_2$가 Tx로부터 같은 거리만큼 떨어져 있을 때 이 두 곳에서 수신한 power는 서로 같을까? 쉬운 예시로 한 가정에서 서로 다른방에 있을 때 수신하는 power는 같을까? 하는 질문이다.
→ 공간이 달라지면 신호가 전송되는 경로가 달라지기 때문에 서로 다른 power를 수신할 것이다.
위 세 가지 예시 모두에서 power는 Instantaneous power가 아니라 Average power를 의미한다. Instantaneous power는 시간에 따라 변하므로 서로 다른 두 Instantaneous power를 비교하기란 매우 복잡하므로 constant로 주어지는 Average power 끼리 비교한다.
Delay Spread and Doppler Spread

Delay spread : Wireless channel에서는 power 감쇠에 더하여 또 한가지 문제점이 있다. Tx에서 $\delta(t)$를 전송하는 경우 received signal은 reflection, diffraction, scattering을 거쳐 서로 다른 delay를 가지고 여러 개의 복사본이 도착한다.
Doppler spread : Rx가 이동한다면 received signal이 변화한다. Rx가 Tx의 방향으로 이동하면 Received signal의 주파수가 증가하고, 반대로 이동하면 주파수가 감소하는 doppler shift 현상이 발생한다. 또한 Rx의 이동속도가 빠를수록 frequency shift가 더 큰 폭으로 발생한다.
즉, mobility에 의해 원본 신호가 가지고 있는 BW가 변화된다.
Delay spread와 Doppler spread의 영향 때문에 Instantaneous power는 매 시간 변화하는 문제가 있다.
Received Signal Power in Wireless Channel

Tx으로부터 같은 거리만큼 떨어진 5개의 구역에서 power를 측정한 것이다. 검정 선은 Instantaneous power를, 빨간선은 time average power를 나타낸다.
즉, Tx로부터 같은 거리만큼 떨어져있다 하더라도 시간에 환경에 따라 Instantaneous power가 매우 다를 수 있고, 그에 따라 average power도 다른 형태를 보인다.
Goal

<Large scale fading model> : Average power
- Path loss : 거리에 따라 power가 얼마나 줄어들 것인지를 나타낸다.
- Shadowing : Path loss로만 modeling을 수행하면 Tx로 부터 떨어진 거리가 서로 같은 경우에는 power가 동일해야 한다. 하지만 실제로는 서로 다른 power가 측정되는데, 이 부분을 수학적으로 modeling하기 위한 요소가 바로 shadowing이다. <path loss와 shadowing은 Average power에 대한 modeling이다.>
<Small scale fading model> : Instantaneous power
- 사람의 목소리는 보통 100~3000Hz의 BW를 가진다. 사람의 음성 신호를 마이크에 입력한 후 fourier transform해보면 서로 다른 BW에서 정의된다. 이때 100~500Hz BW 영역과 500~1000Hz BW 영역에서 channel에 의해 서로 다른 영향을 받는다면, frequency 성분에 의해 서로 다른 영향을 받는 것이므로 이것을 frequency selective channel이라고 한다.
- 보내고자 하는 신호의 모든 BW에 channel이 constant 영향을 미친다면 frequency flat fading이라고 한다.
- Rx가 시간에 따라 계속 움직이는 경우 Time domain에서 diffraction, reflection, scattering의 영향이 계속 바뀌어 channel 또한 바뀌게 된다. 매 시간 간격동안 channel이 Time domain에서 빠르게 변화한다면 fast fading이라고 말하고, channel이 거의 일정하다면 slow fading이라고 말한다.
- Channel이 변화되지 않는 시간 길이를 coherence time이라고 한다.
<Fast fading, slow fading도 Instantaneous power에 대한 modeling이다.>
Path loss in Free Space

Free space에서 Tx와 Rx의 distance $d$가 멀어짐에 따라 $P_r(d)=k\frac{P_t}{d^2}$에 의하여 $d^2$에 따라 power가 감소한다. 이는 실험적으로 증명된 사실이다.
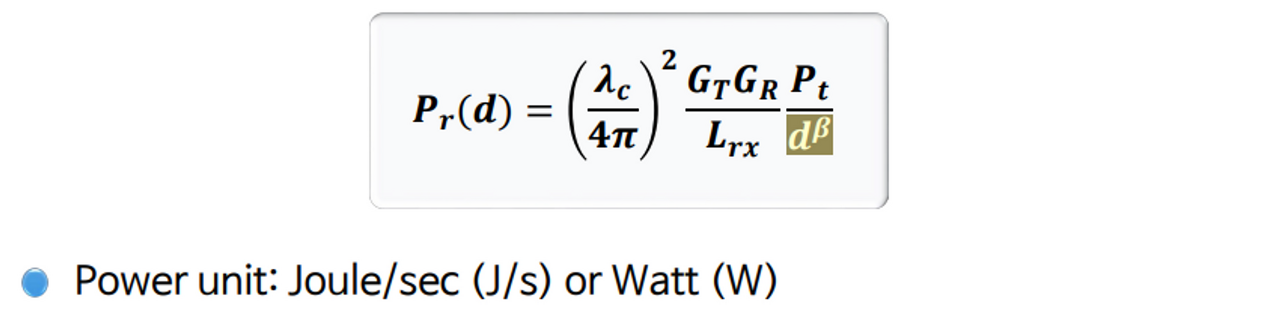
Free space에서는 거리의 제곱만큼 power가 감소했지만, 실제 상황에서는 $d^\beta$에 따라 power가 감소된다. 즉, free space에서는 $\beta=2$였지만, 실제 상황에서는 $\beta$값이 3,4 혹은 8까지도 가능하므로 power가 매우 크게 감소할 수 있다.
- : Tx antenna의 gain
- : Rx antenna의 gain
- $P_t$ : Transmit power
- $L_{rx}$ : receiver에서 발생하는 loss
- $\lambda_c$ : wave length
'이동통신공학' 카테고리의 다른 글
| 3. Large Scale Channel Model:Path Loss and Shadowing (0) | 2023.09.08 |
|---|---|
| 1. Introduction, Spectral & power efficiency, Cellular concept (0) | 2023.09.03 |

